Abstract
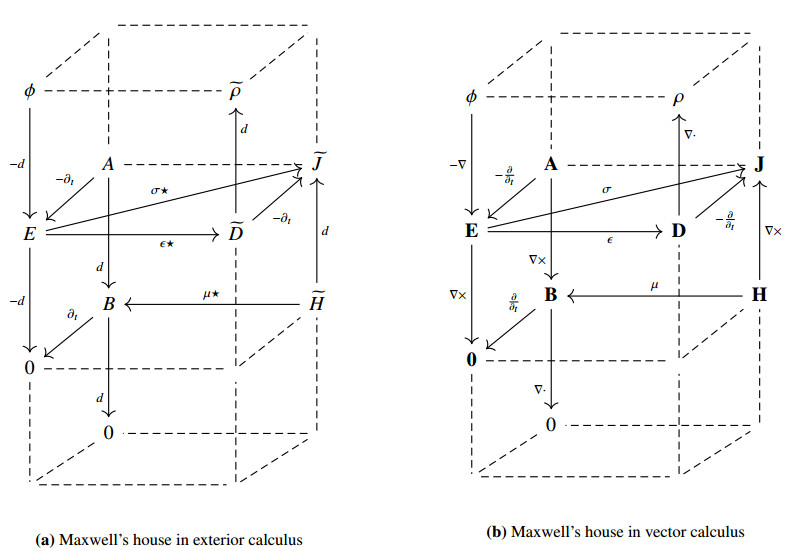
Presenting systems of differential equations in the form of diagrams has become common in certain parts of physics, especially electromagnetism and computational physics. In this work, we aim to put such use of diagrams on a firm mathematical footing, while also systematizing a broadly applicable framework to reason formally about systems of equations and their solutions. Our main mathematical tools are category-theoretic diagrams, which are well known, and morphisms between diagrams, which have been less appreciated. As an application of the diagrammatic framework, we show how complex, multiphysical systems can be modularly constructed from basic physical principles. A wealth of examples, drawn from electromagnetism, transport phenomena, fluid mechanics, and other fields, is included.